决策树
基本算法
决策树分类算法的一般流程如下:
- 一开始,所有的观测均属于根节点,所有特征的取值均离散化;
- 根据启发规则选择一个特征,根据特征取值的不同对观测进行分割;
- 对分割后得到的节点进行同样的启发式特征选择与观测分割过程,如此往复,直到
- 分割得到的观测集合属于同一类;
- 特征用完,以子集中绝大多数的观测类别作为该叶节点的类别
流程中最重要的一个环节是启发规则,本文称之为特征选择规则。在每一个节点进行特征选择时,由于有众多的选项,需要一个选择规则。基本的原则是使最后构造出的决策树规模最小。基于这个基本原则,我们启发式地定义规则为使分割后得到的子节点纯度最大。于是特征选择规则问题就转化为了纯度定义的问题。目前常见的决策树有三种算法,分别对应三种定义:
- ID3:信息增益
- C4.5:信息增益比
- CART:基尼系数
参数选择规则
ID3与信息增益
我们利用熵(Entropy)的概念去描述“不纯度”,熵值越大,说明这个节点的纯度越低:当节点的类别均匀分布时,熵值为1;当只包含一类时,熵值为0.熵的计算公式如下图,以2为底的概率对数与概率乘积之和的相反数。
\[Info(D) = -\sum_{i=1}^mp_i\log_2(p_i)\]
基于熵的概念,我们可以得到特征选择的第一个规则:信息增益(Info Gain)。信息增益的定义是分裂前的节点熵减去分裂后子节点熵的加权和,即不纯度的减少量,也就是纯度的增加量。特征选择的规则是:选择使信息增益最大的特征分割该节点。
我们举一个例子来说明这个概念。
假设我们的数据集如下:
| age | income | student | credit_rating | buys_computer |
|---|---|---|---|---|
| <=30 | high | no | fair | no |
| <=30 | high | no | excellent | no |
| (30,40] | high | no | fair | yes |
| >40 | medium | no | fair | yes |
| >40 | low | yes | fair | yes |
| >40 | low | yes | excellent | no |
| (30,40] | low | yes | excellent | yes |
| <=30 | medium | no | fair | no |
| <=30 | low | yes | fair | yes |
| >40 | medium | yes | fair | yes |
| <=30 | medium | yes | excellent | yes |
| (30,40] | high | yes | fair | yes |
| (30,40] | medium | no | excellent | yes |
| >40 | medium | no | excellent | no |
其中y变量为buys_computer,特征x包括age,income,student,credit_rating。
我们现在根据信息增益来选择下一步要拆分的特征。
拆分前的信息熵\(Info(D)\):9个正例,5个负例
\[Info(D)=I(9,5)=-\frac{9}{14}\log_2\frac{9}{14}-\frac{5}{14}\log_2\frac{5}{14}=0.940\]
按照age特征拆分观测:<=30的正例2个,负例3个,信息熵为\(I(2,3)=0.971\);[31,40)的正例4个,负例0个,信息熵为\(I(4,0)=0\);>40的正例3个,负例2个,信息熵为\(I(3,2)=0.971\)。上述信息汇总为表格如下:
| age | \(p_i\) | \(n_i\) | I(p_i, n_i) |
|---|---|---|---|
| <=30 | 2 | 3 | 0.971 |
| [31,40) | 4 | 0 | 0 |
| > 40 | 3 | 2 | 0.971 |
那么按照age拆分观测的信息为上面各项的加权平均:
\[Info_{age}(D)=\frac{5}{14}I(2,3)+\frac{4}{14}I(4,0)+\frac{5}{14}I(3,2)=0.694\]
那么按照age拆分的信息增益如下:
\[Gain(age)=Info(D) - Info_{age}(D)=0.246\]
同理,按照income、student和credit_rating拆分得到的信息增益分别是:
\[Gain(income)=0.029\] \[Gain(student)=0.151\] \[Gain(credit_rating)=0.048\]
可以看到,选择age划分观测带来的信息增益最大,所以,我们第一个选择的特征是age。
C4.5与信息增益比
信息增益存在的问题是:倾向于选择包含多取值的参数,因为参数的取值越多,其分割后的子节点纯度可能越高。为了避免这个问题,我们引入了增益比例(Gain Ratio)的选择指标,其定义如下:
\[SplitInfo_A(D)=-\sum_{j=1}^{v}\frac{|D_j|}{|D|}\log_2\frac{|D_j|}{|D|}\]
\[GainRatio(A)=Gain(A)/SplitInfo(A)\]
特征A共有\(v\)个取值,宗观测数为\(|D|\);取值为\(j\)的观测数为\(|D_j|\)。从\(SplitInfo_A(D)\)的定义可以看出,当A的取值只有一个时,取值为0;当A的取值有多个,且每个取值的观测数完全一样时,取值最大。因此信息增益比存在的问题是:倾向于选择分割不均匀的分裂方法,举例而言,一个拆分若分为两个节点,一个节点特别多的观测,一个节点特别少的观测,那么这种拆分有利于被选择。
为了克服信息增益和增益比例各自的问题,一个综合性的解决方案如下:首先利用信息增益概念,计算每一个特征分割的信息增益,获得平均信息增益;选出信息增益大于平均值的所有特征集合,对该集合计算信息增益比,选择其中增益比例最大的特征进行决策树分裂。
CART与基尼系数
上面介绍的是基于熵概念的参数选择规则,另一种流行的规则称为基尼指数(Gini Index),其定义如下:
\[gini(D)=1-\sum_{j=1}^np_j^2\]
其中\(n\)是决策树的分类数,在上面提到的例子中为2;\(p_j\)是类别为\(j\)的观测数与D观测数的商。
对于上例,拆分前的基尼系数为:
\[gini(D)=g(9,5)=1-(\frac{9}{14})^2-(\frac{5}{14})^2=0.459\]
按照age拆分的基尼系数为:
\[gini_{age}(D)=\frac{5}{14}g(2,3)+\frac{4}{14}g(4,0)+\frac{5}{14}g(3,2)\]
基尼系数在节点取值分布均匀时取最大值1-1/n,在只包含一个类别时取最小值0. 所以与熵类似,也是一个描述不纯度的指标。
基于基尼系数的规则是:选择不纯度减少量(Reduction in impurity)最大的参数。不纯度减少量是分割前的Gini index减去分割后的Gini index。基尼系数的特点与信息增益的特点类似。
过拟合与剪枝
过度拟合问题是对训练数据完全拟合的决策树对新数据的预测能力较低。为了解决这个问题,有两种解决方法。第一种方法是前剪枝(prepruning),即事先设定一个分裂阈值,若分裂得到的信息增益不大于这个阈值,则停止分裂。第二种方法是后剪枝(postpruning),首先生成与训练集完全拟合的决策树,然后自下而上地逐层剪枝,如果一个节点的子节点被删除后,决策树的准确度没有降低,那么就将该节点设置为叶节点(基于的原则是Occam剪刀:具有相似效果的两个模型选择较简单的那个)。
决策树的优缺点
本节讨论的决策树优缺点摘录自《集成智慧编程》
优点有:
- 最大的优势是易于解释
- 同时接受categorical和numerical数据,不需要做预处理或归一化。
- 允许结果是不确定的:叶子节点具有多种可能的结果值却无法进一步拆分,可以统计count,评估出一个概率。
缺点有:
- 对于只有几种可能结果的问题,算法很有效;面对拥有大量可能结果的数据集时,决策树会变得异常复杂,预测效果也可能会大打折扣。
- 尽管能处理简单的数值型数据,但只能创建满足“大于/小于”条件的节点。若决定分类的因素取决于更多变量的复杂组合,此时要根据决策树进行分类就会比较困难了。例如,假设结果值是由两个变量的差来决定的,那么这棵树会变得异常庞大,而且预测的准确性也会迅速下降。
总而言之:决策树最适合用来处理的,是那些带分界点的、由大量分类数据和数值数据共同组成的数据集。
关于书中提到的假设结果值是由两个变量的差来决定的,那么这棵树会变得异常庞大,而且预测的准确性也会迅速下降,我们可以用下面的例子来实验一下:
library(rpart)
library(rpart.plot)
library(dplyr)
# 生成训练数据
age1 <- as.integer(runif(1000, min=18, max=30))
age2 <- as.integer(runif(1000, min=18, max=30))
df <- data.frame(cbind(age1, age2))
df <- df %>% mutate(diff=age1-age2, label = diff >= 0 & diff <= 5)
ct <- rpart.control(xval=10, minsplit=20, cp=0.01)
# 使用age1与age2预测
cfit <- rpart(label~age1+age2,
data=df, method="class", control=ct,
parms=list(split="gini")
)
rpart.plot(cfit, main="Decision Tree"); 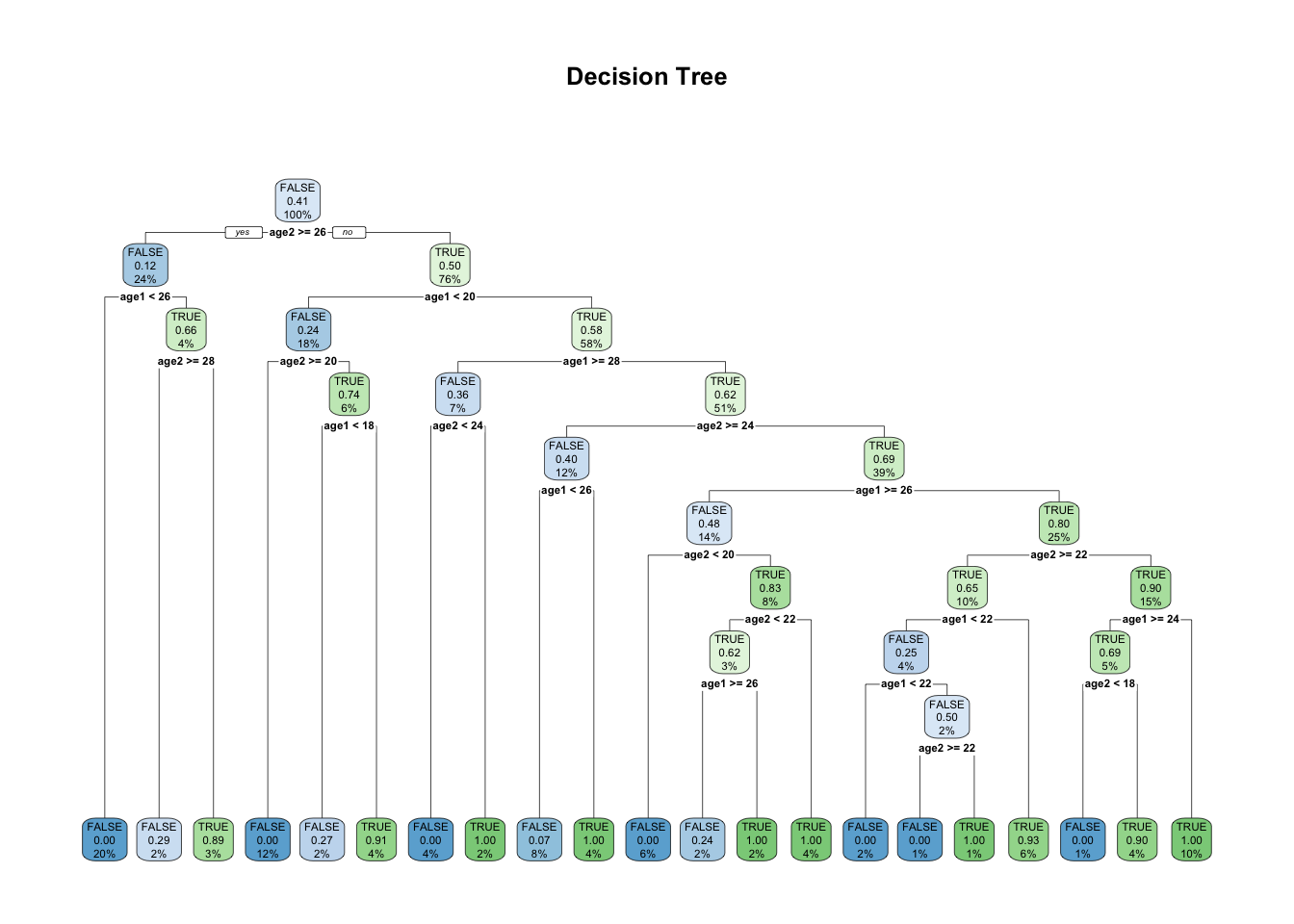
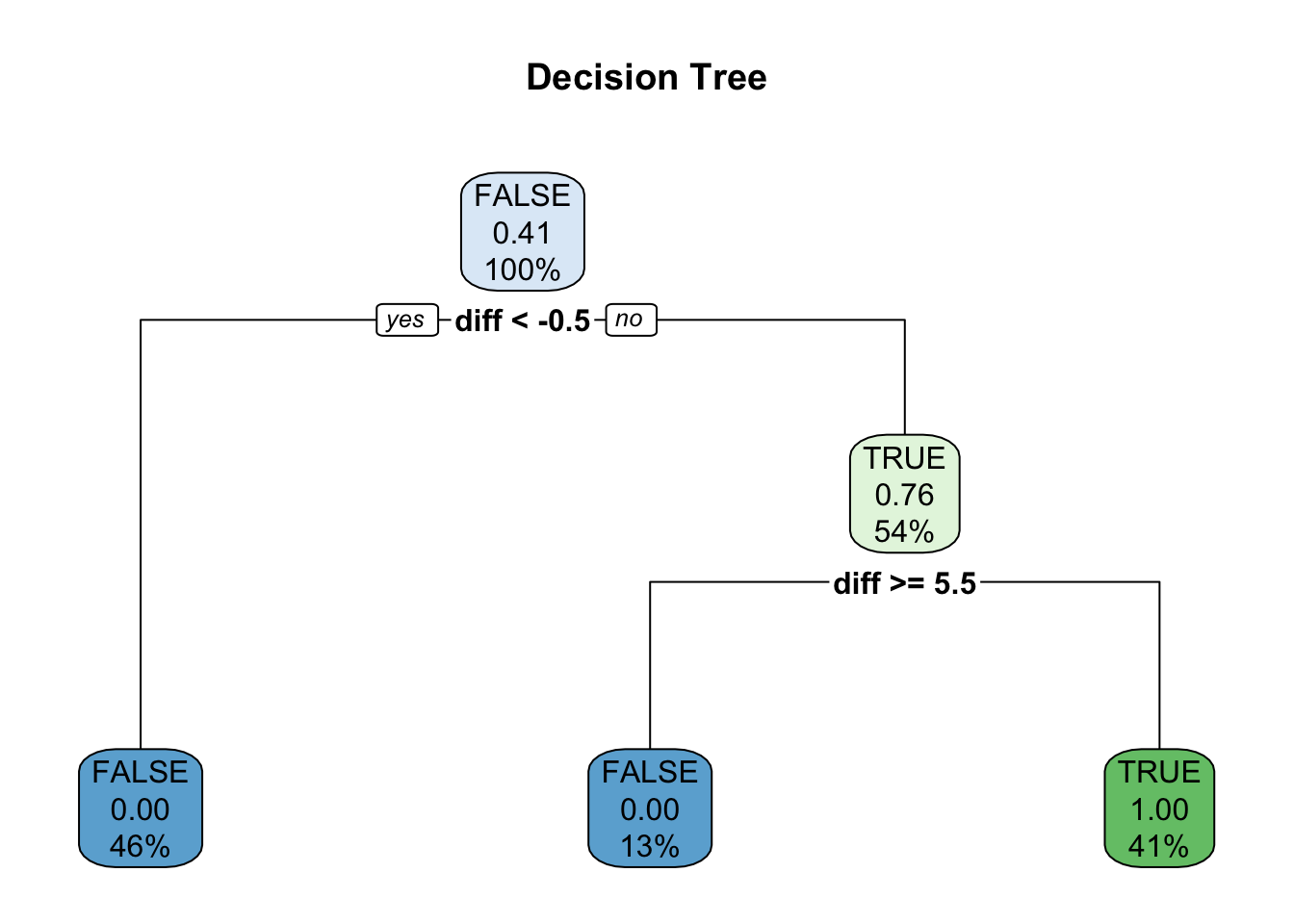
# 使用diff预测
cfit <- rpart(label~diff,
data=df, method="class", control=ct,
parms=list(split="gini")
)
rpart.plot(cfit, main="Decision Tree");